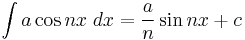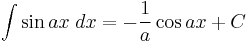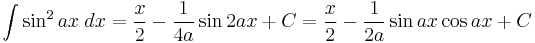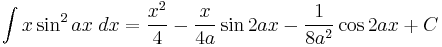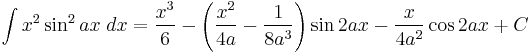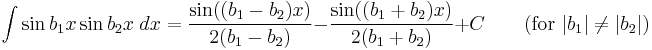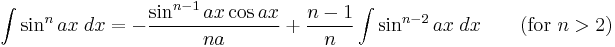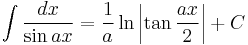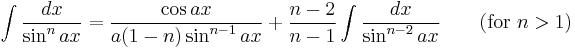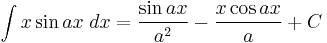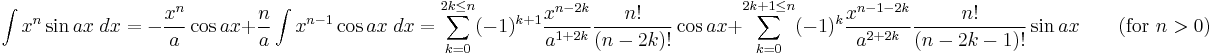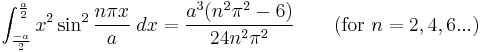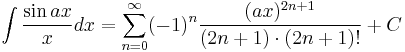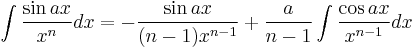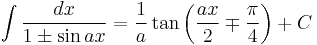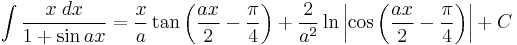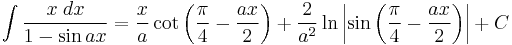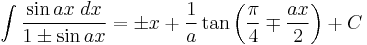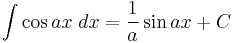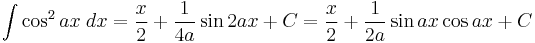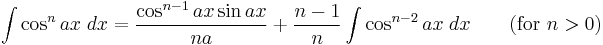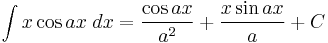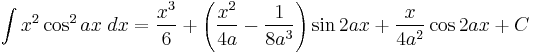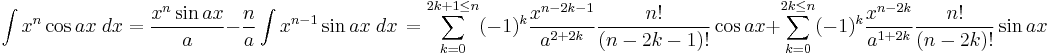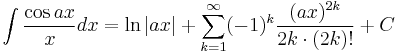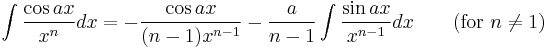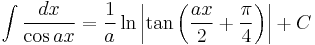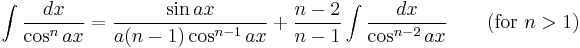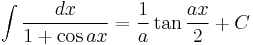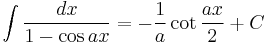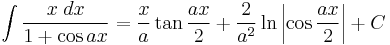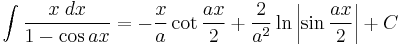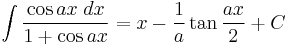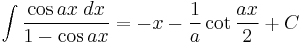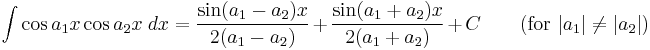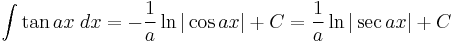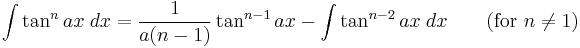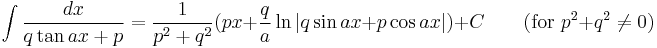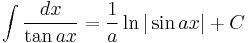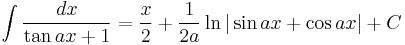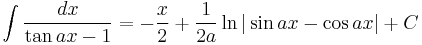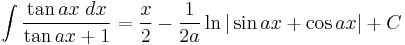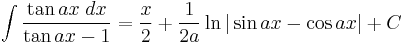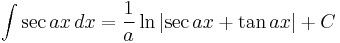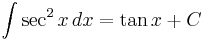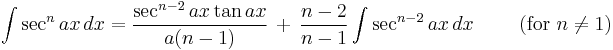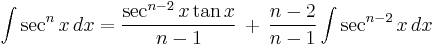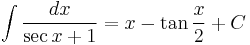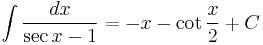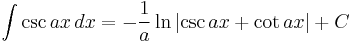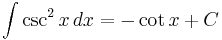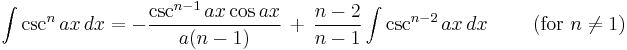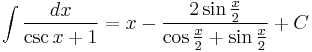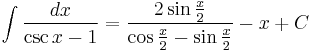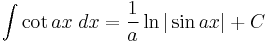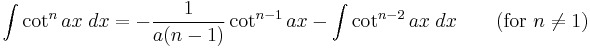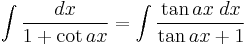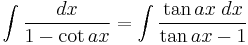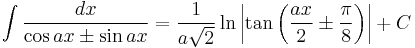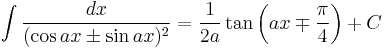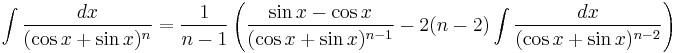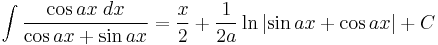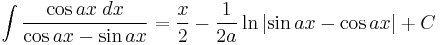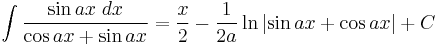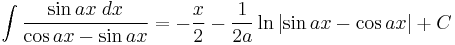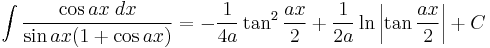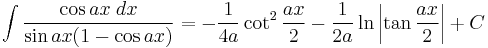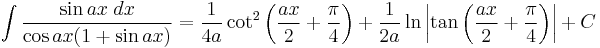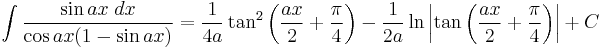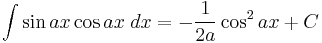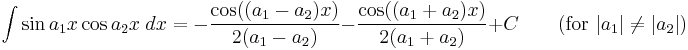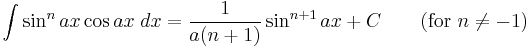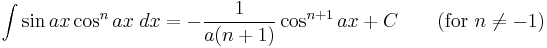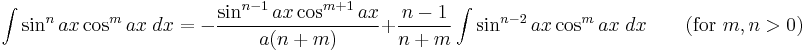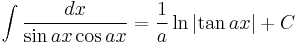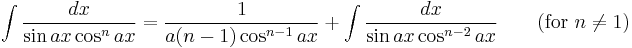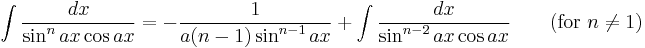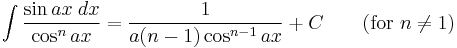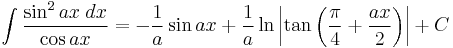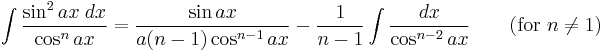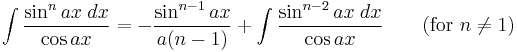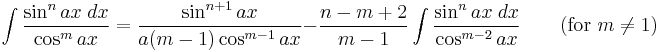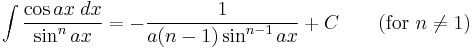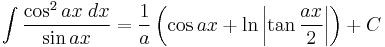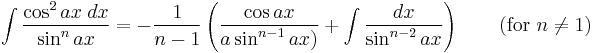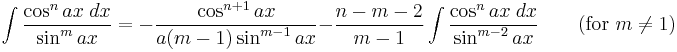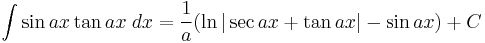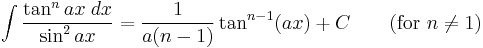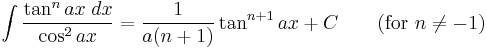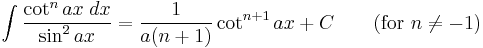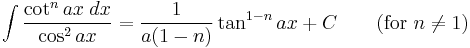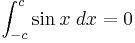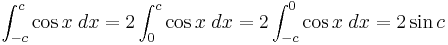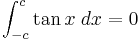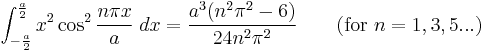List of integrals of trigonometric functions

Trigonometry
History
Usage
Functions
Generalized
Inverse functions
Further reading
Reference
Identities
Exact constants
Trigonometric tables
Laws and theorems
Law of sines
Law of cosines
Law of tangents
Law of cotangents
Pythagorean theorem
Calculus
Trigonometric substitution
Integrals of functions
Derivatives of functions
Integrals of inverse functions

The following is a list of integrals (antiderivative functions) of trigonometric functions. For antiderivatives involving both exponential and trigonometric functions, see List of integrals of exponential functions. For a complete list of antiderivative functions, see lists of integrals. See also trigonometric integral.

Generally, if the function 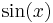\sin(x) is any trigonometric function, and 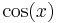\cos(x) is its derivative,

\int a\cos nx\;dx = \frac{a}{n}\sin nx%2Bc

In all formulas the constant a is assumed to be nonzero, and C denotes the constant of integration.

Contents

Integrals involving only sine

\int\sin ax\;dx = -\frac{1}{a}\cos ax%2BC\,\!
\int\sin^2 {ax}\;dx = \frac{x}{2} - \frac{1}{4a} \sin 2ax %2BC= \frac{x}{2} - \frac{1}{2a} \sin ax\cos ax %2BC\!
\int x\sin^2 {ax}\;dx = \frac{x^2}{4} - \frac{x}{4a} \sin 2ax - \frac{1}{8a^2} \cos 2ax %2BC\!
\int x^2\sin^2 {ax}\;dx = \frac{x^3}{6} - \left( \frac {x^2}{4a} - \frac{1}{8a^3} \right) \sin 2ax - \frac{x}{4a^2} \cos 2ax %2BC\!
\int\sin b_1x\sin b_2x\;dx = \frac{\sin((b_1-b_2)x)}{2(b_1-b_2)}-\frac{\sin((b_1%2Bb_2)x)}{2(b_1%2Bb_2)}%2BC \qquad\mbox{(for }|b_1|\neq|b_2|\mbox{)}\,\!
\int\sin^n {ax}\;dx = -\frac{\sin^{n-1} ax\cos ax}{na} %2B \frac{n-1}{n}\int\sin^{n-2} ax\;dx \qquad\mbox{(for }n>2\mbox{)}\,\!
\int\frac{dx}{\sin ax} = \frac{1}{a}\ln \left|\tan\frac{ax}{2}\right|%2BC
\int\frac{dx}{\sin^n ax} = \frac{\cos ax}{a(1-n) \sin^{n-1} ax}%2B\frac{n-2}{n-1}\int\frac{dx}{\sin^{n-2}ax} \qquad\mbox{(for }n>1\mbox{)}\,\!
\int x\sin ax\;dx = \frac{\sin ax}{a^2}-\frac{x\cos ax}{a}%2BC\,\!
\int x^n\sin ax\;dx = -\frac{x^n}{a}\cos ax%2B\frac{n}{a}\int x^{n-1}\cos ax\;dx = \sum_{k=0}^{2k\leq n} (-1)^{k%2B1} \frac{x^{n-2k}}{a^{1%2B2k}}\frac{n!}{(n-2k)!} \cos ax %2B\sum_{k=0}^{2k%2B1\leq n}(-1)^k \frac{x^{n-1-2k}}{a^{2%2B2k}}\frac{n!}{(n-2k-1)!} \sin ax \qquad\mbox{(for }n>0\mbox{)}\,\!
\int_{\frac{-a}{2}}^{\frac{a}{2}} x^2\sin^2 {\frac{n\pi x}{a}}\;dx = \frac{a^3(n^2\pi^2-6)}{24n^2\pi^2} \qquad\mbox{(for }n=2,4,6...\mbox{)}\,\!
\int\frac{\sin ax}{x} dx = \sum_{n=0}^\infty (-1)^n\frac{(ax)^{2n%2B1}}{(2n%2B1)\cdot (2n%2B1)!} %2BC\,\!
\int\frac{\sin ax}{x^n} dx = -\frac{\sin ax}{(n-1)x^{n-1}} %2B \frac{a}{n-1}\int\frac{\cos ax}{x^{n-1}} dx\,\!
\int\frac{dx}{1\pm\sin ax} = \frac{1}{a}\tan\left(\frac{ax}{2}\mp\frac{\pi}{4}\right)%2BC
\int\frac{x\;dx}{1%2B\sin ax} = \frac{x}{a}\tan\left(\frac{ax}{2} - \frac{\pi}{4}\right)%2B\frac{2}{a^2}\ln\left|\cos\left(\frac{ax}{2}-\frac{\pi}{4}\right)\right|%2BC
\int\frac{x\;dx}{1-\sin ax} = \frac{x}{a}\cot\left(\frac{\pi}{4} - \frac{ax}{2}\right)%2B\frac{2}{a^2}\ln\left|\sin\left(\frac{\pi}{4}-\frac{ax}{2}\right)\right|%2BC
\int\frac{\sin ax\;dx}{1\pm\sin ax} = \pm x%2B\frac{1}{a}\tan\left(\frac{\pi}{4}\mp\frac{ax}{2}\right)%2BC

Integrands involving only cosine

\int\cos ax\;dx = \frac{1}{a}\sin ax%2BC\,\!
\int\cos^2 {ax}\;dx = \frac{x}{2} %2B \frac{1}{4a} \sin 2ax %2BC = \frac{x}{2} %2B \frac{1}{2a} \sin ax\cos ax %2BC\!
\int\cos^n ax\;dx = \frac{\cos^{n-1} ax\sin ax}{na} %2B \frac{n-1}{n}\int\cos^{n-2} ax\;dx \qquad\mbox{(for }n>0\mbox{)}\,\!
\int x\cos ax\;dx = \frac{\cos ax}{a^2} %2B \frac{x\sin ax}{a}%2BC\,\!
\int x^2\cos^2 {ax}\;dx = \frac{x^3}{6} %2B \left( \frac {x^2}{4a} - \frac{1}{8a^3} \right) \sin 2ax %2B \frac{x}{4a^2} \cos 2ax %2BC\!
\int x^n\cos ax\;dx = \frac{x^n\sin ax}{a} - \frac{n}{a}\int x^{n-1}\sin ax\;dx\,= \sum_{k=0}^{2k%2B1\leq n} (-1)^{k} \frac{x^{n-2k-1}}{a^{2%2B2k}}\frac{n!}{(n-2k-1)!} \cos ax %2B\sum_{k=0}^{2k\leq n}(-1)^{k} \frac{x^{n-2k}}{a^{1%2B2k}}\frac{n!}{(n-2k)!} \sin ax \!
\int\frac{\cos ax}{x} dx = \ln|ax|%2B\sum_{k=1}^\infty (-1)^k\frac{(ax)^{2k}}{2k\cdot(2k)!}%2BC\,\!
\int\frac{\cos ax}{x^n} dx = -\frac{\cos ax}{(n-1)x^{n-1}}-\frac{a}{n-1}\int\frac{\sin ax}{x^{n-1}} dx \qquad\mbox{(for }n\neq 1\mbox{)}\,\!
\int\frac{dx}{\cos ax} = \frac{1}{a}\ln\left|\tan\left(\frac{ax}{2}%2B\frac{\pi}{4}\right)\right|%2BC
\int\frac{dx}{\cos^n ax} = \frac{\sin ax}{a(n-1) \cos^{n-1} ax} %2B \frac{n-2}{n-1}\int\frac{dx}{\cos^{n-2} ax} \qquad\mbox{(for }n>1\mbox{)}\,\!
\int\frac{dx}{1%2B\cos ax} = \frac{1}{a}\tan\frac{ax}{2}%2BC\,\!
\int\frac{dx}{1-\cos ax} = -\frac{1}{a}\cot\frac{ax}{2}%2BC\,\!
\int\frac{x\;dx}{1%2B\cos ax} = \frac{x}{a}\tan\frac{ax}{2} %2B \frac{2}{a^2}\ln\left|\cos\frac{ax}{2}\right|%2BC
\int\frac{x\;dx}{1-\cos ax} = -\frac{x}{a}\cot\frac{ax}{2}%2B\frac{2}{a^2}\ln\left|\sin\frac{ax}{2}\right|%2BC
\int\frac{\cos ax\;dx}{1%2B\cos ax} = x - \frac{1}{a}\tan\frac{ax}{2}%2BC\,\!
\int\frac{\cos ax\;dx}{1-\cos ax} = -x-\frac{1}{a}\cot\frac{ax}{2}%2BC\,\!
\int\cos a_1x\cos a_2x\;dx = \frac{\sin(a_1-a_2)x}{2(a_1-a_2)}%2B\frac{\sin(a_1%2Ba_2)x}{2(a_1%2Ba_2)}%2BC \qquad\mbox{(for }|a_1|\neq|a_2|\mbox{)}\,\!

Integrands involving only tangent

\int\tan ax\;dx = -\frac{1}{a}\ln|\cos ax|%2BC = \frac{1}{a}\ln|\sec ax|%2BC\,\!
\int\tan^n ax\;dx = \frac{1}{a(n-1)}\tan^{n-1} ax-\int\tan^{n-2} ax\;dx \qquad\mbox{(for }n\neq 1\mbox{)}\,\!
\int\frac{dx}{q \tan ax %2B p} = \frac{1}{p^2 %2B q^2}(px %2B \frac{q}{a}\ln|q\sin ax %2B p\cos ax|)%2BC \qquad\mbox{(for }p^2 %2B q^2\neq 0\mbox{)}\,\!
\int\frac{dx}{\tan ax} = \frac{1}{a}\ln|\sin ax|%2BC\,\!
\int\frac{dx}{\tan ax %2B 1} = \frac{x}{2} %2B \frac{1}{2a}\ln|\sin ax %2B \cos ax|%2BC\,\!
\int\frac{dx}{\tan ax - 1} = -\frac{x}{2} %2B \frac{1}{2a}\ln|\sin ax - \cos ax|%2BC\,\!
\int\frac{\tan ax\;dx}{\tan ax %2B 1} = \frac{x}{2} - \frac{1}{2a}\ln|\sin ax %2B \cos ax|%2BC\,\!
\int\frac{\tan ax\;dx}{\tan ax - 1} = \frac{x}{2} %2B \frac{1}{2a}\ln|\sin ax - \cos ax|%2BC\,\!

Integrands involving only secant

In the 17th century, the integral of the secant function was the subject of a well-known conjecture posed in the 1640s by Henry Bond. The problem was solved by Isaac Barrow.[1] It was originally for the purposes of cartography that this was needed. See Integral of the secant function.

\int \sec{ax} \, dx = \frac{1}{a}\ln{\left| \sec{ax} %2B \tan{ax}\right|}%2BC
\int \sec^2{x} \, dx = \tan{x}%2BC
\int \sec^n{ax} \, dx = \frac{\sec^{n-2}{ax} \tan {ax}}{a(n-1)} \,%2B\, \frac{n-2}{n-1}\int \sec^{n-2}{ax} \, dx \qquad \mbox{ (for }n \ne 1\mbox{)}\,\!
\int \sec^n{x} \, dx = \frac{\sec^{n-2}{x}\tan{x}}{n-1} \,%2B\, \frac{n-2}{n-1}\int \sec^{n-2}{x}\,dx[2]
\int \frac{dx}{\sec{x} %2B 1} = x - \tan{\frac{x}{2}}%2BC
\int \frac{dx}{\sec{x} - 1} = - x - \cot{\frac{x}{2}}%2BC

Integrands involving only cosecant

\int \csc{ax} \, dx = -\frac{1}{a}\ln{\left| \csc{ax}%2B\cot{ax}\right|}%2BC
\int \csc^2{x} \, dx = -\cot{x}%2BC
\int \csc^n{ax} \, dx = -\frac{\csc^{n-1}{ax} \cos{ax}}{a(n-1)} \,%2B\, \frac{n-2}{n-1}\int \csc^{n-2}{ax} \, dx \qquad \mbox{ (for }n \ne 1\mbox{)}\,\!
\int \frac{dx}{\csc{x} %2B 1} = x - \frac{2\sin{\frac{x}{2}}}{\cos{\frac{x}{2}}%2B\sin{\frac{x}{2}}}%2BC
\int \frac{dx}{\csc{x} - 1} = \frac{2\sin{\frac{x}{2}}}{\cos{\frac{x}{2}}-\sin{\frac{x}{2}}}-x%2BC

Integrands involving only cotangent

\int\cot ax\;dx = \frac{1}{a}\ln|\sin ax|%2BC\,\!
\int\cot^n ax\;dx = -\frac{1}{a(n-1)}\cot^{n-1} ax - \int\cot^{n-2} ax\;dx \qquad\mbox{(for }n\neq 1\mbox{)}\,\!
\int\frac{dx}{1 %2B \cot ax} = \int\frac{\tan ax\;dx}{\tan ax%2B1}\,\!
\int\frac{dx}{1 - \cot ax} = \int\frac{\tan ax\;dx}{\tan ax-1}\,\!

Integrands involving both sine and cosine

\int\frac{dx}{\cos ax\pm\sin ax} = \frac{1}{a\sqrt{2}}\ln\left|\tan\left(\frac{ax}{2}\pm\frac{\pi}{8}\right)\right|%2BC
\int\frac{dx}{(\cos ax\pm\sin ax)^2} = \frac{1}{2a}\tan\left(ax\mp\frac{\pi}{4}\right)%2BC
\int\frac{dx}{(\cos x %2B \sin x)^n} = \frac{1}{n-1}\left(\frac{\sin x - \cos x}{(\cos x %2B \sin x)^{n - 1}} - 2(n - 2)\int\frac{dx}{(\cos x %2B \sin x)^{n-2}} \right)
\int\frac{\cos ax\;dx}{\cos ax %2B \sin ax} = \frac{x}{2} %2B \frac{1}{2a}\ln\left|\sin ax %2B \cos ax\right|%2BC
\int\frac{\cos ax\;dx}{\cos ax - \sin ax} = \frac{x}{2} - \frac{1}{2a}\ln\left|\sin ax - \cos ax\right|%2BC
\int\frac{\sin ax\;dx}{\cos ax %2B \sin ax} = \frac{x}{2} - \frac{1}{2a}\ln\left|\sin ax %2B \cos ax\right|%2BC
\int\frac{\sin ax\;dx}{\cos ax - \sin ax} = -\frac{x}{2} - \frac{1}{2a}\ln\left|\sin ax - \cos ax\right|%2BC
\int\frac{\cos ax\;dx}{\sin ax(1%2B\cos ax)} = -\frac{1}{4a}\tan^2\frac{ax}{2}%2B\frac{1}{2a}\ln\left|\tan\frac{ax}{2}\right|%2BC
\int\frac{\cos ax\;dx}{\sin ax(1-\cos ax)} = -\frac{1}{4a}\cot^2\frac{ax}{2}-\frac{1}{2a}\ln\left|\tan\frac{ax}{2}\right|%2BC
\int\frac{\sin ax\;dx}{\cos ax(1%2B\sin ax)} = \frac{1}{4a}\cot^2\left(\frac{ax}{2}%2B\frac{\pi}{4}\right)%2B\frac{1}{2a}\ln\left|\tan\left(\frac{ax}{2}%2B\frac{\pi}{4}\right)\right|%2BC
\int\frac{\sin ax\;dx}{\cos ax(1-\sin ax)} = \frac{1}{4a}\tan^2\left(\frac{ax}{2}%2B\frac{\pi}{4}\right)-\frac{1}{2a}\ln\left|\tan\left(\frac{ax}{2}%2B\frac{\pi}{4}\right)\right|%2BC
\int\sin ax\cos ax\;dx = -\frac{1}{2a}\cos^2 ax %2BC\,\!
\int\sin a_1x\cos a_2x\;dx = -\frac{\cos((a_1-a_2)x)}{2(a_1-a_2)} -\frac{\cos((a_1%2Ba_2)x)}{2(a_1%2Ba_2)} %2BC\qquad\mbox{(for }|a_1|\neq|a_2|\mbox{)}\,\!
\int\sin^n ax\cos ax\;dx = \frac{1}{a(n%2B1)}\sin^{n%2B1} ax %2BC\qquad\mbox{(for }n\neq -1\mbox{)}\,\!
\int\sin ax\cos^n ax\;dx = -\frac{1}{a(n%2B1)}\cos^{n%2B1} ax %2BC\qquad\mbox{(for }n\neq -1\mbox{)}\,\!
\int\sin^n ax\cos^m ax\;dx = -\frac{\sin^{n-1} ax\cos^{m%2B1} ax}{a(n%2Bm)}%2B\frac{n-1}{n%2Bm}\int\sin^{n-2} ax\cos^m ax\;dx \qquad\mbox{(for }m,n>0\mbox{)}\,\!
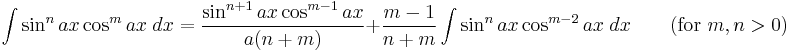
also: \int\sin^n ax\cos^m ax\;dx = \frac{\sin^{n%2B1} ax\cos^{m-1} ax}{a(n%2Bm)} %2B \frac{m-1}{n%2Bm}\int\sin^n ax\cos^{m-2} ax\;dx \qquad\mbox{(for }m,n>0\mbox{)}\,\!
\int\frac{dx}{\sin ax\cos ax} = \frac{1}{a}\ln\left|\tan ax\right|%2BC
\int\frac{dx}{\sin ax\cos^n ax} = \frac{1}{a(n-1)\cos^{n-1} ax}%2B\int\frac{dx}{\sin ax\cos^{n-2} ax} \qquad\mbox{(for }n\neq 1\mbox{)}\,\!
\int\frac{dx}{\sin^n ax\cos ax} = -\frac{1}{a(n-1)\sin^{n-1} ax}%2B\int\frac{dx}{\sin^{n-2} ax\cos ax} \qquad\mbox{(for }n\neq 1\mbox{)}\,\!
\int\frac{\sin ax\;dx}{\cos^n ax} = \frac{1}{a(n-1)\cos^{n-1} ax} %2BC\qquad\mbox{(for }n\neq 1\mbox{)}\,\!
\int\frac{\sin^2 ax\;dx}{\cos ax} = -\frac{1}{a}\sin ax%2B\frac{1}{a}\ln\left|\tan\left(\frac{\pi}{4}%2B\frac{ax}{2}\right)\right|%2BC
\int\frac{\sin^2 ax\;dx}{\cos^n ax} = \frac{\sin ax}{a(n-1)\cos^{n-1}ax}-\frac{1}{n-1}\int\frac{dx}{\cos^{n-2}ax} \qquad\mbox{(for }n\neq 1\mbox{)}\,\!
\int\frac{\sin^n ax\;dx}{\cos ax} = -\frac{\sin^{n-1} ax}{a(n-1)} %2B \int\frac{\sin^{n-2} ax\;dx}{\cos ax} \qquad\mbox{(for }n\neq 1\mbox{)}\,\!
\int\frac{\sin^n ax\;dx}{\cos^m ax} = \frac{\sin^{n%2B1} ax}{a(m-1)\cos^{m-1} ax}-\frac{n-m%2B2}{m-1}\int\frac{\sin^n ax\;dx}{\cos^{m-2} ax} \qquad\mbox{(for }m\neq 1\mbox{)}\,\!
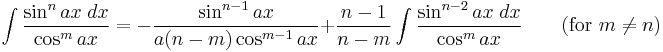
also: \int\frac{\sin^n ax\;dx}{\cos^m ax} = -\frac{\sin^{n-1} ax}{a(n-m)\cos^{m-1} ax}%2B\frac{n-1}{n-m}\int\frac{\sin^{n-2} ax\;dx}{\cos^m ax} \qquad\mbox{(for }m\neq n\mbox{)}\,\!
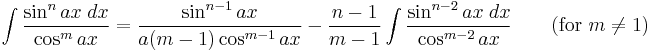
also: \int\frac{\sin^n ax\;dx}{\cos^m ax} = \frac{\sin^{n-1} ax}{a(m-1)\cos^{m-1} ax}-\frac{n-1}{m-1}\int\frac{\sin^{n-2} ax\;dx}{\cos^{m-2} ax} \qquad\mbox{(for }m\neq 1\mbox{)}\,\!
\int\frac{\cos ax\;dx}{\sin^n ax} = -\frac{1}{a(n-1)\sin^{n-1} ax} %2BC\qquad\mbox{(for }n\neq 1\mbox{)}\,\!
\int\frac{\cos^2 ax\;dx}{\sin ax} = \frac{1}{a}\left(\cos ax%2B\ln\left|\tan\frac{ax}{2}\right|\right) %2BC
\int\frac{\cos^2 ax\;dx}{\sin^n ax} = -\frac{1}{n-1}\left(\frac{\cos ax}{a\sin^{n-1} ax)}%2B\int\frac{dx}{\sin^{n-2} ax}\right) \qquad\mbox{(for }n\neq 1\mbox{)}
\int\frac{\cos^n ax\;dx}{\sin^m ax} = -\frac{\cos^{n%2B1} ax}{a(m-1)\sin^{m-1} ax} - \frac{n-m-2}{m-1}\int\frac{\cos^n ax\;dx}{\sin^{m-2} ax} \qquad\mbox{(for }m\neq 1\mbox{)}\,\!
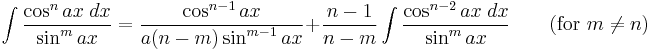
also: \int\frac{\cos^n ax\;dx}{\sin^m ax} = \frac{\cos^{n-1} ax}{a(n-m)\sin^{m-1} ax} %2B \frac{n-1}{n-m}\int\frac{\cos^{n-2} ax\;dx}{\sin^m ax} \qquad\mbox{(for }m\neq n\mbox{)}\,\!
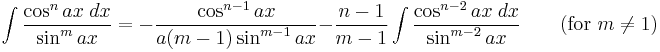
also: \int\frac{\cos^n ax\;dx}{\sin^m ax} = -\frac{\cos^{n-1} ax}{a(m-1)\sin^{m-1} ax} - \frac{n-1}{m-1}\int\frac{\cos^{n-2} ax\;dx}{\sin^{m-2} ax} \qquad\mbox{(for }m\neq 1\mbox{)}\,\!

Integrands involving both sine and tangent

\int \sin ax \tan ax\;dx = \frac{1}{a}(\ln|\sec ax %2B \tan ax| - \sin ax)%2BC\,\!
\int\frac{\tan^n ax\;dx}{\sin^2 ax} = \frac{1}{a(n-1)}\tan^{n-1} (ax) %2BC\qquad\mbox{(for }n\neq 1\mbox{)}\,\!

Integrands involving both cosine and tangent

\int\frac{\tan^n ax\;dx}{\cos^2 ax} = \frac{1}{a(n%2B1)}\tan^{n%2B1} ax %2BC\qquad\mbox{(for }n\neq -1\mbox{)}\,\!

Integrals containing both sine and cotangent

\int\frac{\cot^n ax\;dx}{\sin^2 ax} = \frac{1}{a(n%2B1)}\cot^{n%2B1} ax %2BC\qquad\mbox{(for }n\neq -1\mbox{)}\,\!

Integrands involving both cosine and cotangent

\int\frac{\cot^n ax\;dx}{\cos^2 ax} = \frac{1}{a(1-n)}\tan^{1-n} ax %2BC\qquad\mbox{(for }n\neq 1\mbox{)}\,\!

Integrals with symmetric limits

\int_{{-c}}^{{c}}\sin {x}\;dx = 0 \!
\int_{{-c}}^{{c}}\cos {x}\;dx = 2\int_{{0}}^{{c}}\cos {x}\;dx = 2\int_{{-c}}^{{0}}\cos {x}\;dx = 2\sin {c} \!
\int_{{-c}}^{{c}}\tan {x}\;dx = 0 \!
\int_{-\frac{a}{2}}^{\frac{a}{2}} x^2\cos^2 {\frac{n\pi x}{a}}\;dx = \frac{a^3(n^2\pi^2-6)}{24n^2\pi^2} \qquad\mbox{(for }n=1,3,5...\mbox{)}\,\!

References

  1. ^ V. Frederick Rickey and Philip M. Tuchinsky, "An Application of Geography to Mathematics: History of the Integral of the Secant", Mathematics Magazine, volume 53, number 3, May 2980, pages 162–166
  2. ^ Stewart, James. Calculus: Early Transcendentals, 6th Edition. Thomson: 2008